convexHull
Convex hull of Delaunay triangulation
Description
Examples
2-D Delaunay Triangulation
Compute and plot the convex hull of a 2-D Delaunay triangulation.
Create a Delaunay triangulation from a set of 2-D points.
rng default;
x = rand([10,1]);
y = rand([10,1]);
DT = delaunayTriangulation(x,y);Compute the convex hull.
C = convexHull(DT);
Plot the triangulation and highlight the convex hull in red.
plot(DT.Points(:,1),DT.Points(:,2),'.','MarkerSize',10) hold on plot(DT.Points(C,1),DT.Points(C,2),'r')

3-D Delaunay Triangulation
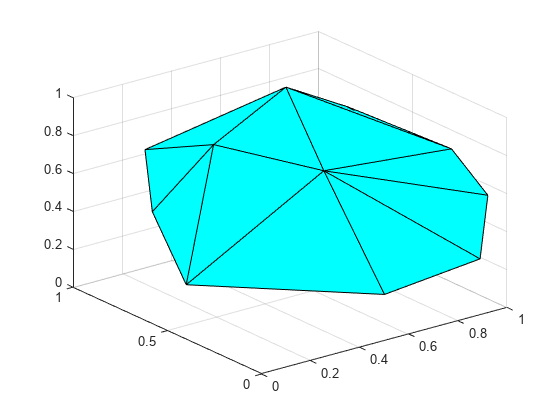
Compute and plot the convex hull of a 3-D Delaunay Triangulation.
Create a Delaunay triangulation from a 3-D set of points.
rng('default');
P = rand([25,3]);
DT = delaunayTriangulation(P);Compute the convex hull and the volume bounded by the convex hull.
[C,v] = convexHull(DT);
Display the volume and plot the convex hull.
v
v = 0.3943
trisurf(C,DT.Points(:,1),DT.Points(:,2),DT.Points(:,3), ... 'FaceColor','cyan')
Input Arguments
DT — Delaunay triangulation
scalar
Delaunay triangulation, specified as a scalar delaunayTriangulation
object.
Data Types: delaunayTriangulation
Output Arguments
C — Convex hull vertices
column vector | matrix
Convex hull vertices, returned as a column vector or matrix of vertex IDs.
When
DTis a 2-D triangulation,Cis a column vector containing the sequence of vertex IDs around the convex hull. The vertex IDs are the row numbers of the vertices in thePointsproperty.When
DTis 3-D triangulation,Cis a 3-column matrix containing the connectivity list of triangle vertices in the convex hull.
Data Types: double
v — Area or volume
scalar
Area or volume of the convex hull, returned as a scalar.
Data Types: double
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
Version History
Introduced in R2013a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)